今回は矩形波生成ブロックを設計します。
AY-3-8910 の矩形波生成ブロックは、12bit の分周比 N によって クロックを分周させ、さらに 1/16 のプリスケーラと組み合わせることで、fck/16/N の周波数を生成します。
・・・とデータシートに書かれているのですが、出力のデューティー比は 50% にするため、回路上は 1/8 のプリスケーラと 1/2 のポストスケーラによって構成されているものと思います。
PSG 音源にはデューティー比を可変する機能はないので、これは単なる 1/N 分周器(プログラマブル分周器)によって構成できます。
プログラマブル分周器はいろいろな回路が考えられますが、
TTL IC を組み合わせて作るので、部品点数、在庫、価格など
いろいろ考えて設計しなければいけません。
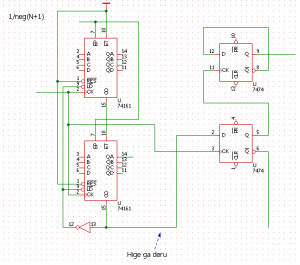
上図は 74LS161 を使用した完全同期式のプログラマブル分周器で、プリセットに N の論理反転を入力することで、1/(N+1) 分周器として働きます。
(上図ではデューティー 50% にするため、さらに 1/2 していますが。)
161 は 4bit カウンタなので、8bit や 12bit で動作させる場合、複数個組み合わせて使用します。
上図のように CO 端子から出力を取ろうとすると、複数個組み合わせた場合ひげが出てしまうので、一度元のクロックで同期してやる必要があります。
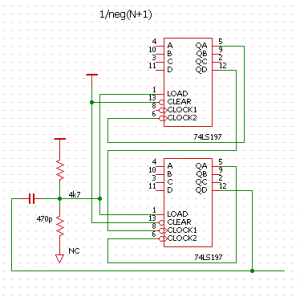
74LS197 のような、安価な非同期式のカウンタで構成した例が上図です。74LS197 にはキャリー出力がないので、MSB の立下りエッジでカウンタをロードしています。ロードは非同期なので、出力周波数はひとつ上の回路と同様になります。
今回は 1/(N+1) ではなく 1/N の分周器を作る必要があります。上記回路では、論理反転のほかに算術 -1 する回路を追加せねばならず、不適です。
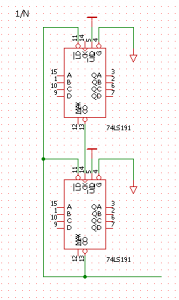
1/N カウンタの実現方法のひとつは、ダウンカウンタを使用することです。74LS191 を使用した 1/N 分周器を上図に示します。74LS193 でも同様です。この回路でも動くと思いますが、MSB のCO 出力はマルチバイブレータ等でパルス拡張した方がベターでしょう。
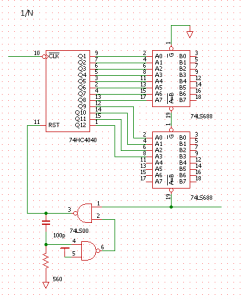
もう一つの構成として、ディジタルコンパレータを使用する回路が考えられます。上記は 74HC4040 によるリプルカウンタの出力を 74LS688 によるコンパレータで比較して、一致でカウンタにリセットをかけています。リセットは非同期なので、結果として出力周波数は 1/N となります。
コンパレータが比較的高価で、配線数も多くなるのでこの方式はあまり採用されませんが、今回は手持ち部品の都合上、この回路をベースに設計します。
そういうわけで、矩形波生成ブロックは上図のような回路になりました。AY-3-8910 には 3 系統の矩形波ブロックが存在するので、上記回路を3つ作ることになります。
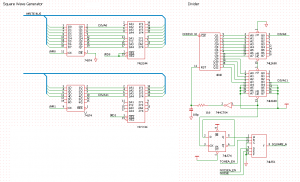
74LS51の入力はAND->NORですからC、FがGNDだと常に0になるような…と思ったら公開されている回路図では修正してあるのですね
途中で気づいた回路の間違いはいくつかあり、blog は修正前のままになっていることがあります。
すみません。
作りながら設計したので IC の無駄が多く、本当はいくつか IC の数を減らせるはずです。